微信红包与博弈游戏

前几天过年抢红包发红包十分欢乐，于是某天晚上我突然想到了一个十分好的提议，看起来我制定了一个不错的游戏规则：

1、两个人同时互相发给对方一个红包，金额是 1 元到 20 元之间的整数；

2、同时拆开红包，发红包少的人要给另一个人补偿 10 元的红包。

当然后来朋友把这些钱退还了回来，不过我们开始进行详细的讨论。我们先将游戏规则重述并稍微简化了一下：两人同时出 1 元到 20 元之间的金额，并且我们都假设金额为整数，出资额小的一方要给对方 10 元钱。看起来这样的游戏规则制定相当合理。

一开始，我想到了博弈论中的经典案例囚徒困境，但是很快发现这并非囚徒困境。因为在我们的假设中，游戏是一个零和博弈，而囚徒困境却是非零和的情况。

我问朋友如果再来一局你会出多少钱？他说他会出 10 元。事实上当我把对话截图发到朋友圈中之后，还真有不止一位朋友评论到可以尝试出 10 元。不过，难道 10 元会是一个最佳选择吗？另外，再假设如果我猜对方会发 10 元，那么我就会出 11 元，以此类推那么我应该出的最理性的数值是 20 元？或者我会觉得 10 元以上会有损失，以此类推那么最理性的数值会是 1 元吗？换一个角度来问，从经济学的角度，在上述我的游戏假设中是否存在一个利益最大点？

我们试着穷举一下 1 元到 20 元的，朋友画了一个简单的图。能从图中看出来点什么吗？看来，概率是一样的！也即我的游戏规则的制定还是相当公平的，惩罚为 10 元相当合理。

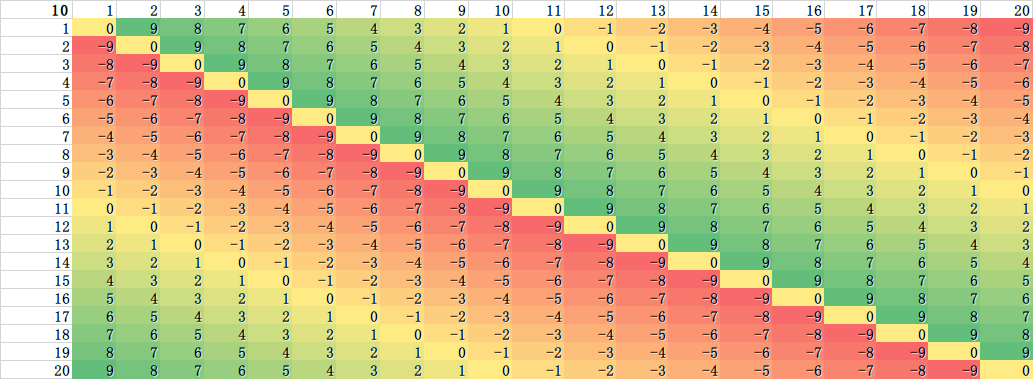
（惩罚为10元的情况）

因此这个问题看起来更像是一个心理学问题，而非经济学问题。因为预期的收益都是一样的，关键还是要判断对方的出牌策略。

继续烧脑。假设双方都是纯理性，那么如果惩罚为 5 元呢？我们继续画收益矩阵。很明显，出的越高，预期收益越低，收益的最大值也越低，所以最佳选择是 1 元。进一步说，只要惩罚数目在 10 元以下，均衡态总是 1 元。那么，如果惩罚为 15 元呢？那么最佳选择就是 20 元。进一步，只要惩罚大于 10 元（且小于 20 元），均衡态总是 20 元。

等一下！真的是这样吗？假设惩罚为 5 元，这个时候不应该用 1 元到 20 元等概率去考虑这个问题，而是 1 元到 10 元等概率，这样就不能说最优选择是 1 元了，而是，在这个区间内就变成了均衡态，也即 1 元到 10 元间的均衡！如果惩罚为 15 元呢？那么就是 11 元到 20 元的均衡。

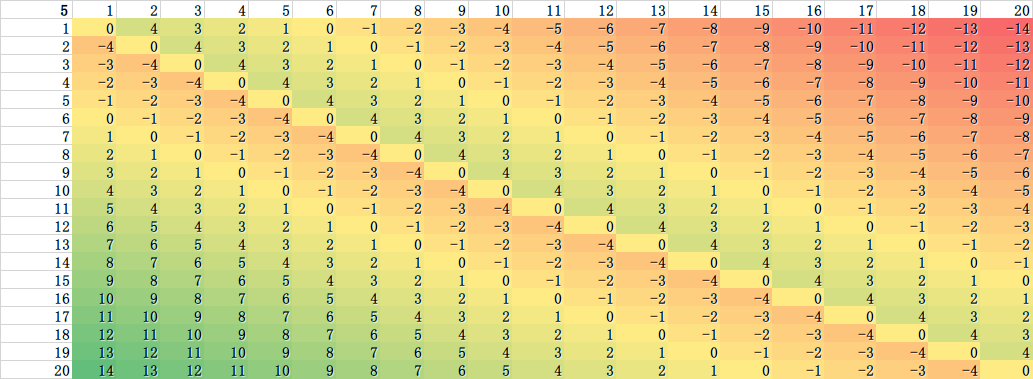
（惩罚为 5 元的情况）

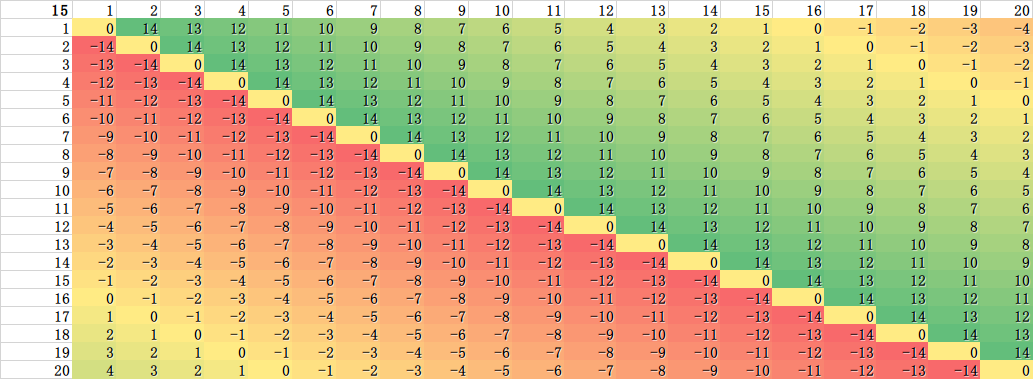
（惩罚为 15 元的情况）

这就是当时我们的思路，大概只讨论到了这里，接着去翻了翻书，恶补了一点博弈学的知识，另外有同学还跟我提到了钱包悖论，乍一看有很多相似，但是仔细看似乎并不是一个内容。后来朋友还去知乎上提问了，不过似乎没有看到十分靠谱的回答。

最后，我去给我在台湾教我们产业经济学（博弈论）的老师写了一封邮件。不得不感叹台湾的老师实在太好了，很快就给了我回复。我觉得老师的思路和我们很不一样，我们在罗列收益矩阵，他却使用求导的方法。老师回信说这个问题不太适合用赛局矩阵来回答，因为参赛者的策略选项太多了，甚至数不清。

在附件中，老师列出了这个问题的详细解答办法。真的挺后悔当时没好好听课，而且看到最后那一串求导的式子，我的头还真有点大，在纸上算了很久，毕竟已经很久没有接触了。

感觉还有一点没有想明白的地方。我觉得老师的这个解答也只是一个简单的思路，并没有展开来说，可能今后还需要继续想一想。作者绝对菜鸟水平，欢迎大家讨论。:)